Does the hat tessellation have a three fold rotational symmetry?
a large tiling of over 2375 hat monotiles has a c3point group
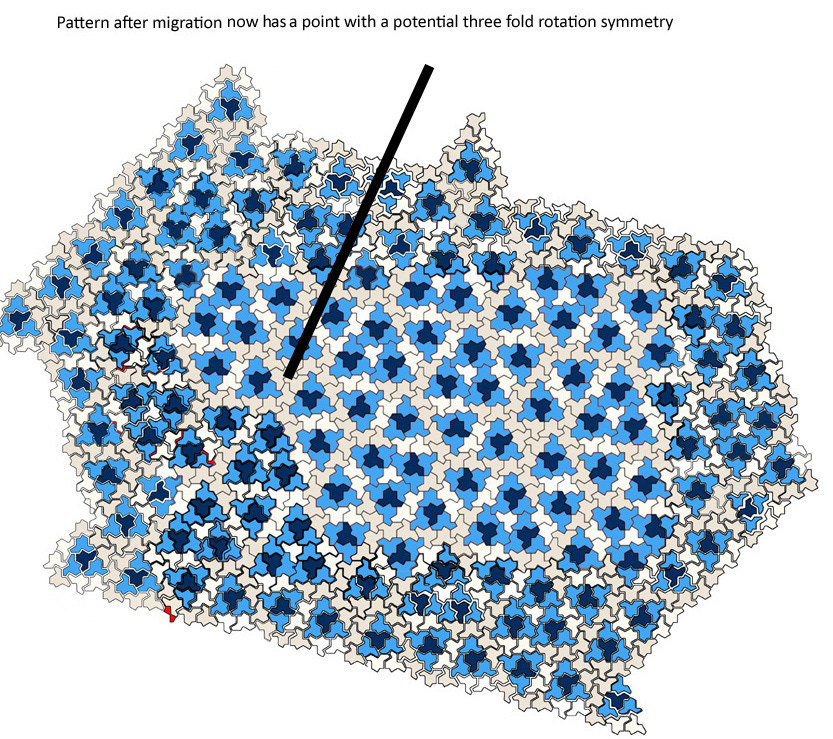
The fragment of the hat tile tessellation reported on the Guardian website, is a pattern which looks as if it may have a threefold axis of rotational symmetry about one point at the center of a six tile grey triangle. To test this, I expanded the pattern avoiding any gaps then made three copies of my extended pattern, which are superimposed each rotated by 120deg (each with 33% transparency) about the point the tentative threefold axis passes through. The result shows that the growing pattern does have point group symmetry C3, at least as far as it is developed
Emphasizing the threefold point symmetry by placing it at the center of the expanding pattern gives
:Further expansion is possible without gaps forming, retaining the threefold symmetry about the center point, making it probable that the whole tessellation of the plane has this symmetry
:Note that only one of the grey triangles in the whole pattern can have a three-fold rotation axis, it is a unique point in the whole tessellated space. The pattern has a point group symmetry. If there were another of the grey triangles also with a threefold axis of symmetry, then the pattern would inevitably form a space group and would contain translational symmetry, forming a lattice, and so be a periodic structure with a unit cell.
If your eye follows the rows of single, 4tile triangles one sees what appear to be repeating patterns suggesting a unit cell linking the centers of the grey triangles of six grey tiles and fixing the ratio of 4tile to 13tile triangles at 13:4 = 3.25
But the pattern does not form a 2D lattice. There is no translational symmetry forcing the pattern to constantly repeat. The dark blue hat orientations vary, i.e there are repeated changes of orientations of the triangles which break the translational symmetry. For the hat tile, the 3.25 ratio is the unique combination which produces tessellation. All other ratios will leave a gap somewhere. For this ratio there is no unit cell smaller than the whole pattern, as the pattern never exactly repeats even as it is extended to cover the whole flat plane. Wallpaper with this pattern would be very frustrating to hang as the pattern at the edges of each roll would never match up!
If molecules packed like this we would get a quasicrystal which could give both sharp and diffuse X-ray diffraction spots – it is not disordered like a liquid, but nor is it ordered like a crystalline solid but it has more order than an amorphous glass.
Another note added later:
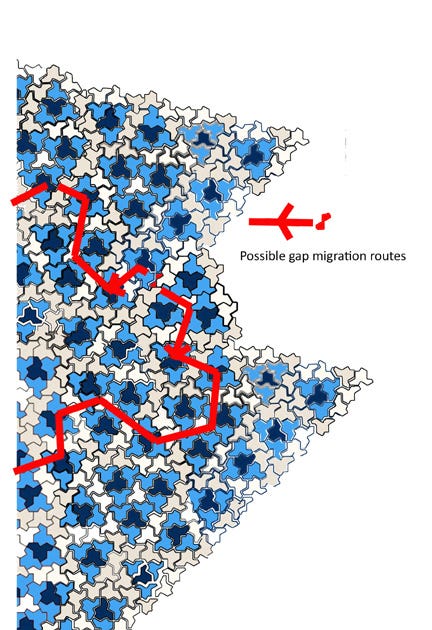
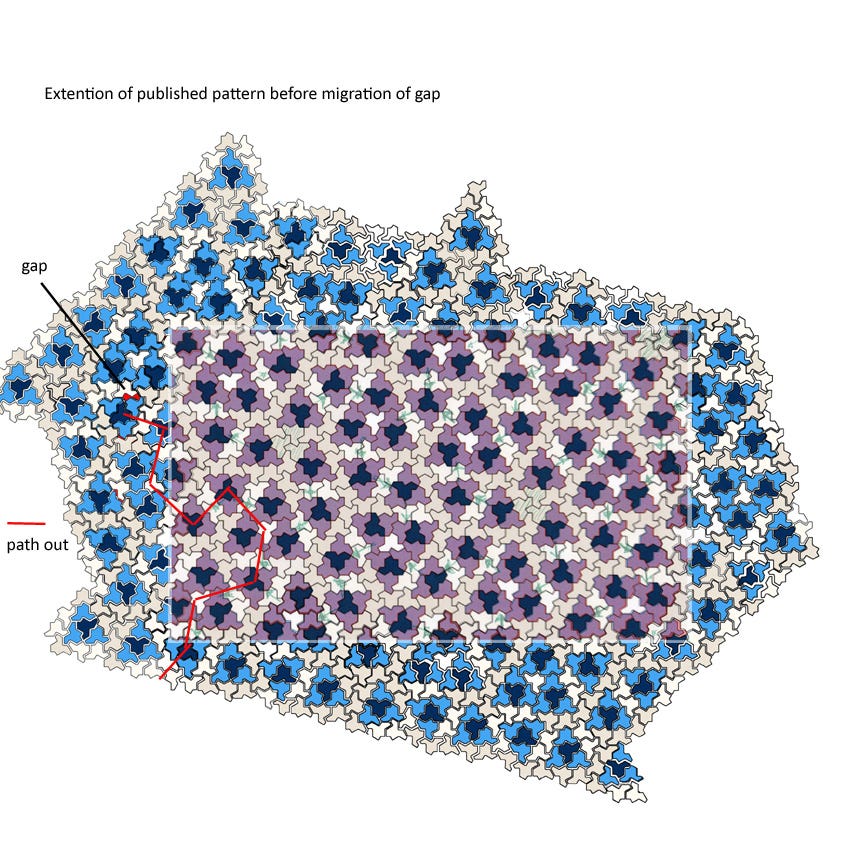
The further expansion of the pattern which gave the C3 point group symmetry tiling of about 2375 tiles, encountered a problem. The three shorter sides of 10, 4-tile triangles, force the continuation shown below. This produces a gap which cannot be migrated out of the pattern by local adjustments of the surrounding tiles
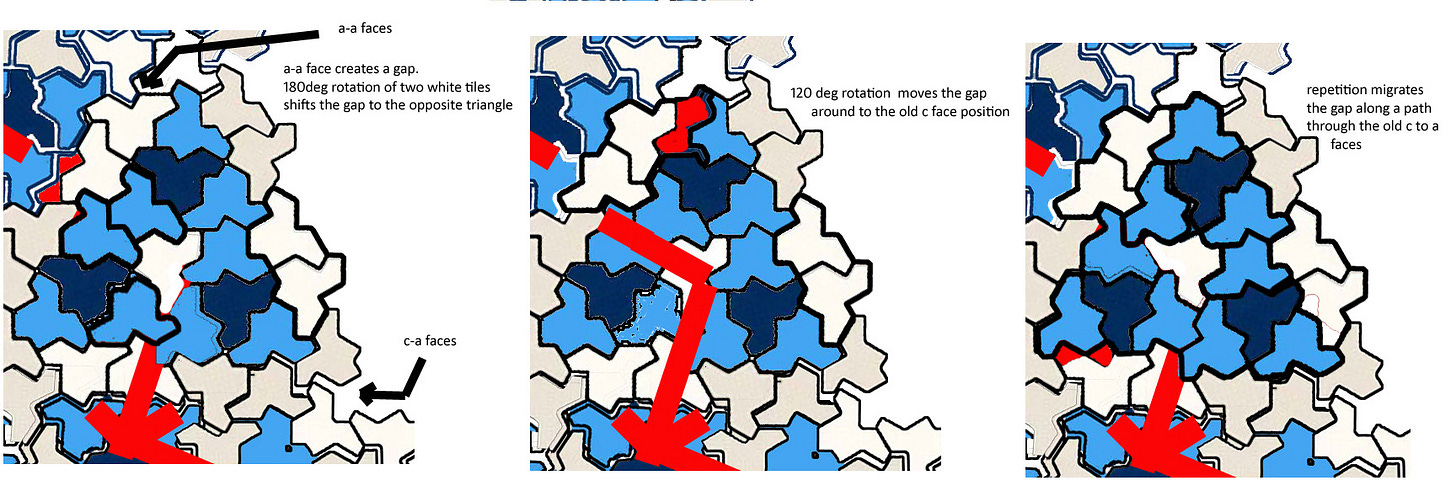
.My continuation of the reported fragment of the tessellating pattern must have deviated from the true pattern at some point. That occurred early on, when a gap appeared and I migrated it out. For gap migration see the red double diamond, which is moved by performing a 180deg rotation of two neighboring white tiles which allows the gap to hop from one triangle to the triangle opposite, across an a-a edge facing space. Rotating the tile 120deg migrates the gap round the triangles edge to face another triangle. If there is a sequence of a-c edges forming a path to the edge of the growing pattern the gap can be eliminated, otherwise it is trapped and the pattern cannot tessellate.
So my C3 point group symmetry pattern does not tessellate.
Comparing my pattern (blue) to the reported tessellating pattern (red), which is overlaid with 50% transparency, shows that six triangles in the lower left corner were rotated by 120 deg, so the central hat orientations differ for those six. Without that there would have been gaps in my hexagonal pattern
.Conclusion : My C3 R3.25 pattern cannot tessellate. But can the tessellation have C3 point group symmetry?
My expansion of the tessellating fragment threw up a gap which I migrated out of the pattern leading to the C3 non tessellating pattern
.An alternative to eliminate the gap is to adopt a different continuation of the pattern which doesn’t interfere with the original fragment . A continuation which maintains the single files of 4tile triangles and notes that the number of such triangles between the six tile grey triangles depends on the grey triangles relative orientation: same (both point down or up) 5, 4tile triangles; different (up-down or down-up) 4 such triangles. The rule to avoid a-a facing edges is followed throughout. A unique continuation of the fragment is then found:
This pattern does not have a potential three fold rotational axis anywhere within its boundary so cannot give a tiling with the C3 point group symmetry. But this pattern does tessellate the plane with no gaps and without forming a 2-d lattice.